Subgraph In-Out Trees

Formally, we define an in-out-tree is the union of an in-tree (anti-arborescence) with an out-tree (arborescence) where both trees share the same root node.

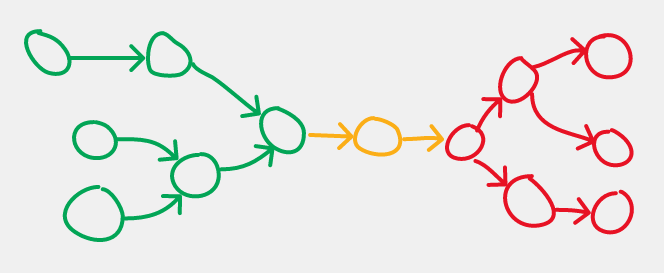An in-out tree graph. Data flows from the green pull operators on the left, through the yellow pivot, and to the red push operators on the right.

In this graph representation, each node corresponds to an operator, and the edges direct the flow of data between operators.

Converting Graph

Any graph can be partitioned into in-out trees. Any non-trivial graph will have many possible partitionings to choose from; a useful heuristic is to partition the graph into as few subgraphs as possible, in order to minimize scheduling overheads.

Most graphs are pretty simple and can be partitioned with a bit of eye-balling. To do this systematically, we can use a simple coloring algorithm.

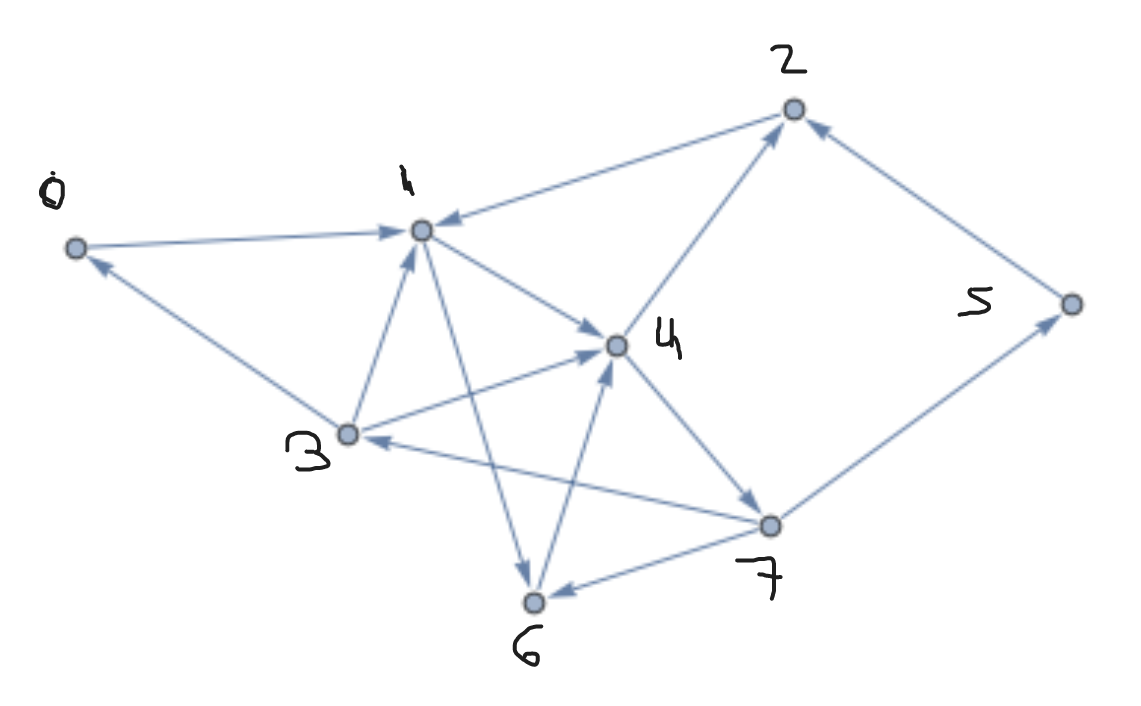An example directed graph.

To identify the in-out trees in an arbitrary directed graph, first identify any nodes which have multiple inputs and outputs and mark these as pull-to-push pivots (yellow in the example). Mark any nodes with multiple inputs (and a single output) as pull (green) and any nodes with multiple outputs as push (red).

In the example:

Pivots (yellow)	Pulls (green)	Pushes (red)
1, 4	2	3, 7

Finally any one-in-one-out nodes should be marked the same as their neighbors (either green pull or red push). If we have green pull -> red push that becomes a yellow pivot. And if red push -> green pull that becomes a blue handoff node, and this is a division between subgraphs. Note that a subgraph can have a handoff with itself; this forms a loop.

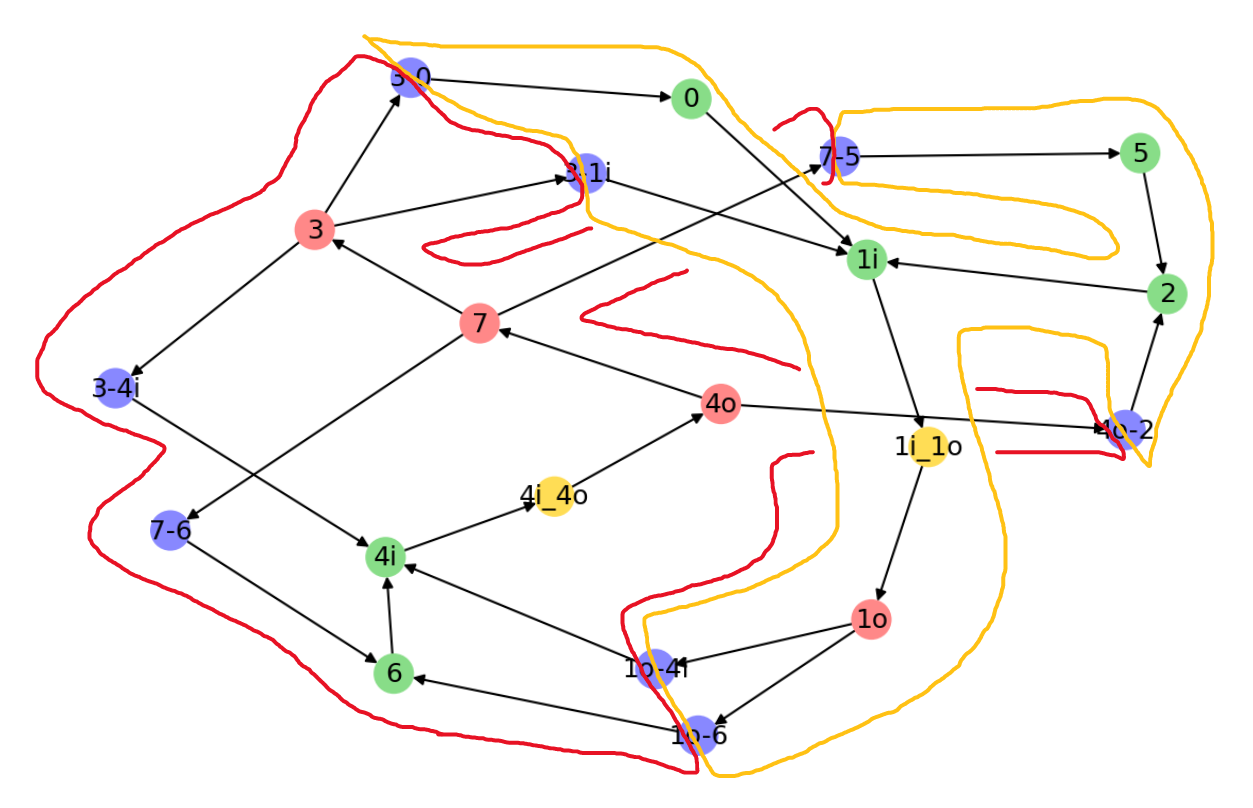The graph above converted and partitioned into two in-out trees. One is outlined in yellow and the other in red. For the corresponding DFIR graph, green nodes are pull, red nodes are push, yellow are pivots, and blue are handoffs.

In the example partitioning above, some nodes have been split into multiple and labelled with suffixes to make the pivots and handoffs more explicit.